今天我们来说说大名鼎鼎的“贝塞尔曲线”。
先看一个 GIF 图，有一个直观的印象（图中红色的线段即为一条贝塞尔曲线）：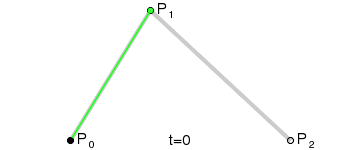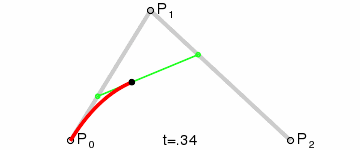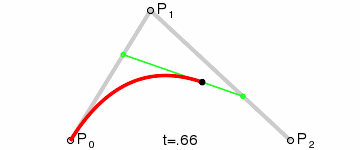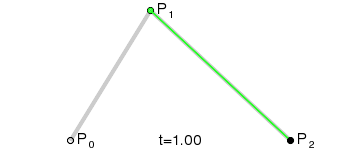

接下来，我们来分析贝塞尔曲线的原理：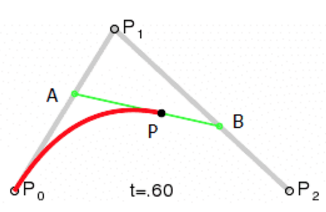

曲线一共有 3 个关键点，P0，P1，P2，其中 P0 和 P2 为数据点，P1 为控制点。
在时间 t 从 0 到 1 的增加的过程中，点 A 从 P0 向 P1 移动，点 B 从 P1 向 P2 移动，连接 A B 两点，点 P 从 A 向 B 移动，如果点 A，B，P 满足以下条件：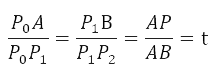

则点 P 的轨迹构成一条贝塞尔曲线。

非常优美的公式，非常好理解，看一遍就懂。
但是，根据这个公式并不能绘制出贝塞尔曲线，我们需要知道 P 点的轨迹方程，那么，这个轨迹方程如何来求呢？

求 P0P1 的轨迹方程

我们先求 P0P1 的方程，P0，P1，A 点的坐标如图所示：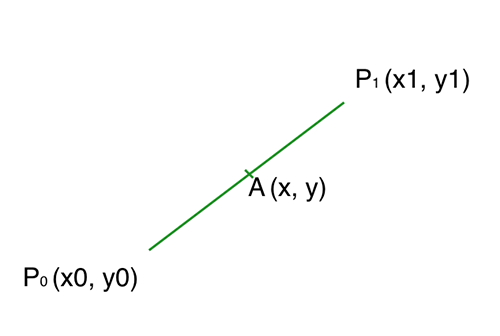

在前面一节，我们得知线段 P0A 的长度除以线段 P0P1 的长度等于 t，这即是说 P0A 的长度等于 P0P1 乘以 t，对应到公式：

1
2
P0A / P0P1 = t (t∈[0,1])
P0A = P0P1 * t (t∈[0,1])

很显示，A 点的坐标满足一个以 t 为自变量的直线方程：

1
A = P0 + t * (P1 - P0) (t∈[0,1])

所以，A 点的 x 和 y 坐标也满足上述直线方程：

1
2
Ax = x0 + t * (x1 - x0) (t∈[0,1])
Ay = y0 + t * (y1 - y0) (t∈[0,1])

同理，可以得到 B 点的 x 和 y 坐标也满足直线方程：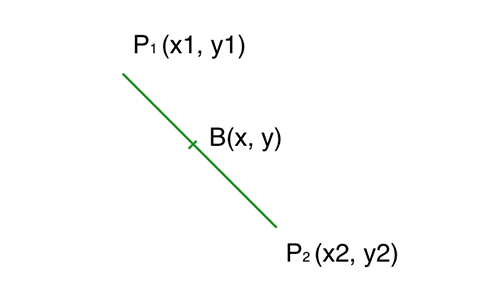

1
2
Bx = x1 + t * (x2 - x1) (t∈[0,1])
By = y1 + t * (y2 - y1) (t∈[0,1])

P 点的坐标 x 和 y 也满足直线方程：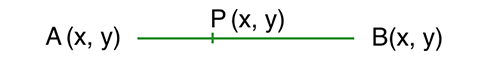

1
2
Px = Ax + t * (Bx - Ax) (t∈[0,1])
Py = Ay + t * (By - Ay) (t∈[0,1])

将 Ax Bx 的方程代入 Px 可以得到 P 点 x 坐标关于时间 t 的方程：

1
2
Px = x0 + t * (x1 - x0) + t * (x1 + t * (x2 - x1) - (x0 + t * (x1 - x0))) (t∈[0,1])
Px = (x2 - 2 * x1 + x0) * t^2 + (x1 - x0) * 2 * t + x0 (t∈[0,1])

同理，也可以得到 P 点 y 坐标关于时间 t 的方程：

1
Py = (y2 - 2 * y1 + y0) * t^2 + (y1 - y0) * 2 * t + y0 (t∈[0,1])

这个方程等价于大家在网上搜到的贝塞尔曲线的方程:

1
Py = (1 - t)^2 * y0 + 2 * (1 - t) * t * y1 + t^2 * y2 (t∈[0,1])

显然，贝塞尔曲线的 x 和 y 坐标的轨迹方程均为一条抛物线，根据这个方程，我们可以粗放地绘出一条贝塞尔曲线。

贝塞尔曲线碰撞检测

接下来，我们来看看，如何判断一个坐标点是否在贝塞尔曲线上，这在做曲线与其它物体的碰撞检测时非常有用。
由上节的推导可知，若点在贝塞尔曲线上，则点的 x 和 y 坐标都要满足我们刚才推导出的抛物线方程。
以点的 x 坐标为例，x 满足抛物线方程，意味着自变量 t 从 0 到 1 增长的过程，抛物线方程的值域包含了 x 这个值。这句话也可以理解为，直线方程 x = at^2 + bt + c (t∈[0,1]) 有解，有解意味着这条抛物线与 t 轴至少有 1 个交点 tx。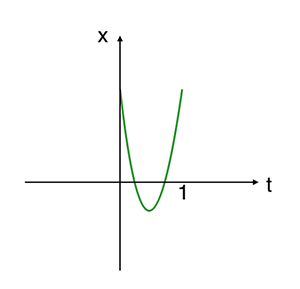

同理，将 y 坐标代入抛物线方程得 y = at^2 + bt + c (t∈[0,1]) 也必须有解，即这条抛物线与 t 轴也至少有 1 个交点ty。
假设在 x 和 y 都满足抛物线方程，且都有解时，如果它们的解有 1 个是相同的，即 tx = ty，则证明在时间 tx 这个时刻，贝塞尔曲线上对应的点的坐标是(x, y)，即这个点在贝塞尔曲线上。